我有一个关于齿轮寿命计算的疑问。我想知道在计算齿轮寿命时,寿命的失效率是多少?是百分之一(1%失效,99%可靠) 还是千分之一(0.1%失效)?
Hanspeter Dinner(KISSsoft全球销售总监)给出了解答。

根据ISO、DIN和AGMA标准评估齿轮时,额定寿命或循环次数的许用应力是从S-N曲线上计算得到的。S-N曲线本身是根据上述标准中提到的过程确定的,仅使用了几个值去描述S-N曲线(如,疲劳极限和材料类型)。基础的S-N曲线是在不同齿轮实验室中测量得到的,如:在慕尼黑技术大学,测量了齿轮强度的有限寿命和无限寿命。
测量得到的原始S-N曲线是基于Pa=50%的失效率。很明显,这么高的失效率在大多数情况下是不适合用于齿轮设计的,并且上面标准中提到的S-N曲线有更低的失效率或更高的可靠度。在那里,安全系数S=1的失效率Pa=1%是基础。这就意味着如果使用安全系数S=1,那么在额定载荷下每100个齿轮中就有一个齿轮会在设计寿命内失效。
这种Pa=1%的失效率可能比需要的要高,或者可能比需要的要低。如果有更高的要求(例如:直升机传动,失效后果是灾难性的),应使用S>1的安全系数,从而减小疲劳极限的循环次数。如果有较低的要求(如,低成本的电动工具齿轮箱),在齿轮设计中疲劳极限可以使用更高的循环次数,导致低成本下有更小的齿轮并且接受更高的失效率。
因此,将疲劳极限转换为其它可靠性水平是有意义的,如在齿轮评定标准中的失效率Pa=1%或可靠度Pu=99%。在AGAM2001系列标准中使用KR系数进行这一转换,但DIN3990和ISO6336中并没有这个系数。下面提到了一些指导原则,如何将数值转换到ISO6336(和DIN3990)下不同等级的可靠性,这是基于下面列出的参考资料和一些数据统计中给出的强度值的分散情况。
齿根和齿面的S-N曲线:
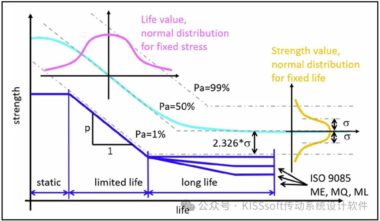
S-N曲线的概念。S-N曲线是在存活率或可靠性Pü=50%时进行测量的。相应的,失效率也是相同的值Pa=50%。它们是在常数应力下有限寿命区域内达到寿命时使用分布来测量的(在那里曲线有斜率p)和无限寿命区域内达到的应力等级的分布(试验齿轮不再失效),使用疲劳极限应力的标准差σ表示(见图1)。达到的寿命的分布远远大于无限寿命下达到的应力的分布。下面的解释适用于无限寿命区。
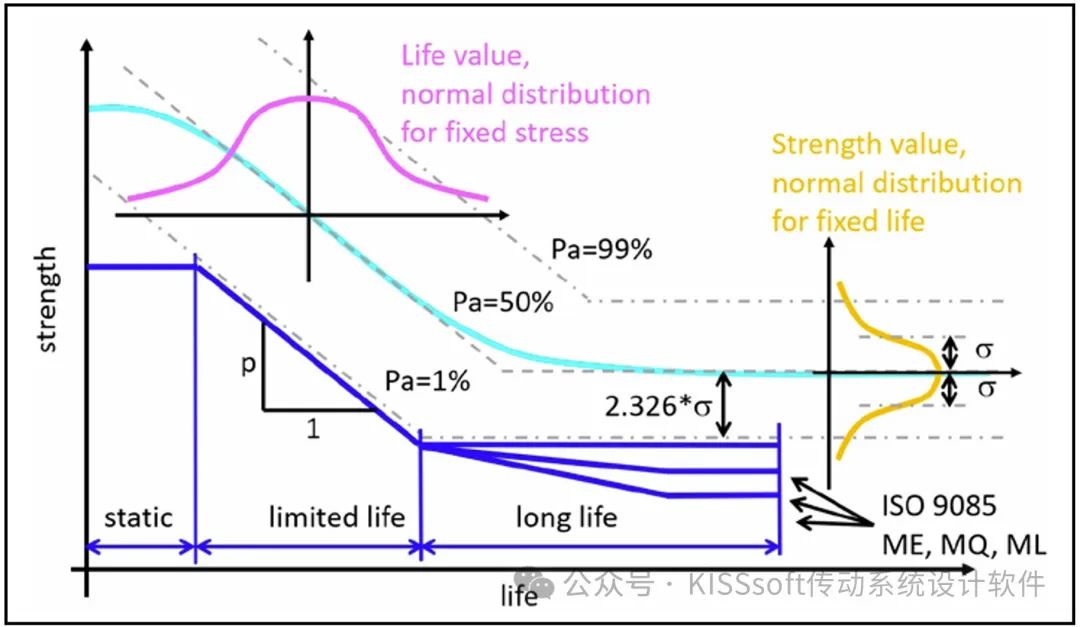
如果有大量的测量数据可用,可以确定S-N曲线(不仅对于Pu=50%),同样,例如,Pu=10%和Pu=90%作为上下边界。另外,其它可靠性下的S-N曲线可以从Pu=50%的S-N曲线和基于文献的标准差σ估算得到(应基于大量的其它试验)。S-N曲线的转换系数,或者说齿根和齿面的疲劳极限,从一个可靠性等级到另一个,已形成报告(见参考文献6-11)并在下文做了解释。
ISO6336中的失效率,S-N曲线:ISO6336-5(见参考文献1-2)中给出的齿面和齿根的疲劳极限,σHlim和σFlim,的失效率是Pa=1%。因此存活率(或可靠性)是Pü=1-Pa=99%。这个值对应于安全系数S=1。
ISO6336-5:2016(见参考文献2)中允许σHlim和σFlim用于其他可靠度等级。这表明,统计分析能够调整这些值,以便与其他损坏概率相对应。然后,当需要其它失效率(可靠性)时,σHlim、σFlim和σFE的值可通过一个合适的“可靠性系数”调整。当进行调整时,应增加注脚表明相关的百分比(如,σHlim10表明失效率10%)。本文推荐使用ISO 12107中描述的方法(见参考文献3)。
ISO 6336没有给出关于如何计算其他可靠性水平的疲劳极限的进一步指导。对于疲劳极限的转换,例如,从1%到10%的失效率,没有给出公式或因素。
AGMA2001中的可靠性系数:在这个标准中,疲劳极限是从试验室测试和现场累积经验中确定或估算出的。它们是基于统一过载系数、1000万次应力循环、单向载荷和99%的可靠性。这就意味着S-N曲线的失效率与ISO6336和DIN3990中的一样。
然而,AGMA2001系列(见参考文献4-5)在这方面规定更详细,在齿轮可靠性等级评定时它引入了一个系数。可靠性系数KR(在AGMA2101中是Yz,见参考文献5):它可以用于修正其它可靠性等级的疲劳极限。据报道,这个数据是基于美国海军(U.S Navy)研发的数据(见表1)。
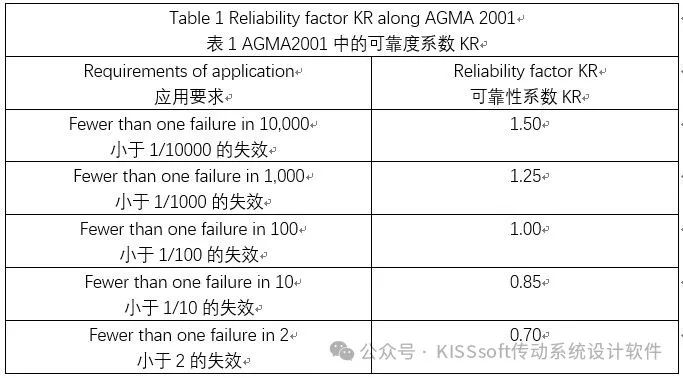
根据AGMA标准中列出的sat或sac值(适用于Pa=1%)除以上述可靠性系数KR,计算出所需可靠性的齿根sat和齿面sac的疲劳极限值。如果可靠性以数量级大的方式增加,那么可靠性系数就会以或多或少的线性增加(见图2)。
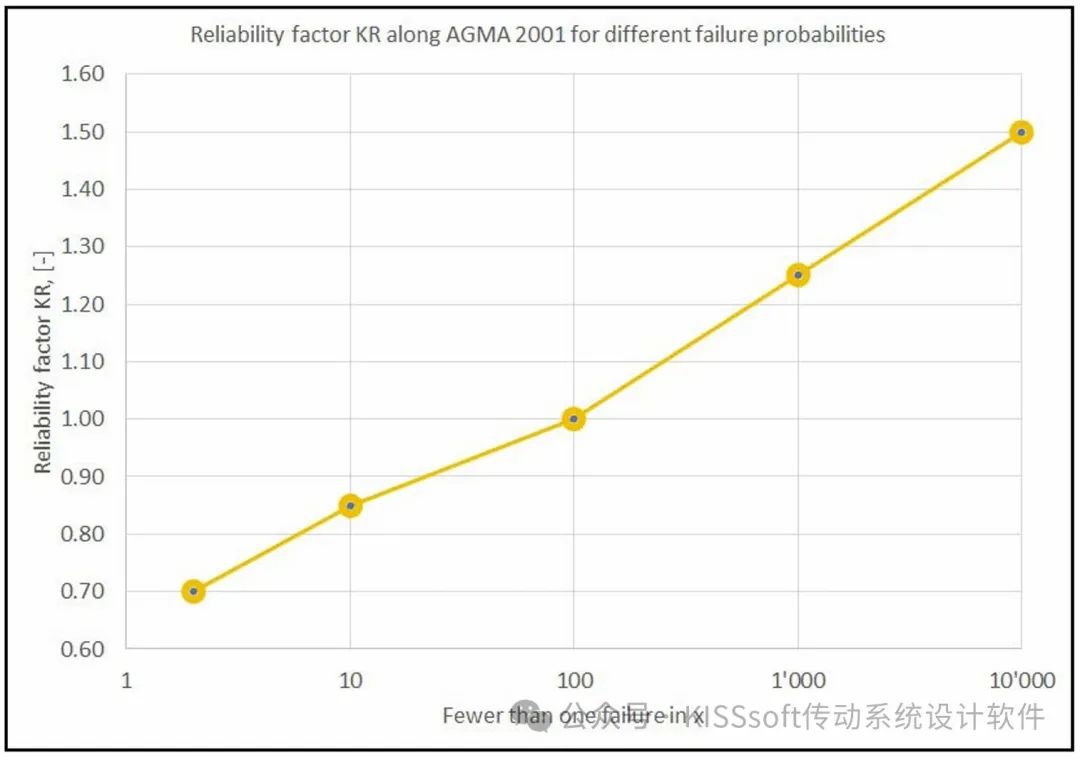
不同可靠性下的疲劳极限:
将疲劳极限转换为可靠性50%以外的值。在ISO6336(或DIN和AGMA标准)中,在Pü=50%下测量得到数据是需要被转换到存活率Pü=99%。50%失效率的齿面σHlim和齿根σFlim的疲劳极限可以使用系数fxH和fxF转换为x%的失效率,如下(见参考文献9):
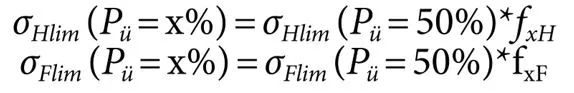
下面列出了X%=99%下的fxH和fxF的值(见表2和表3)。这些值来源不同(它们都来自德国),但是它们可能都基于相同的数据基础。
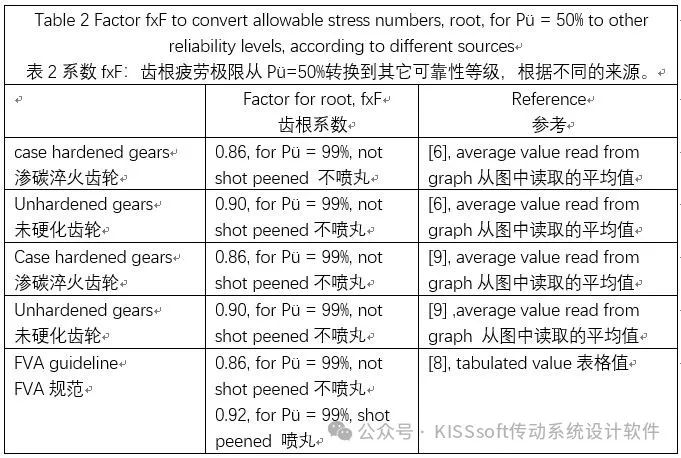
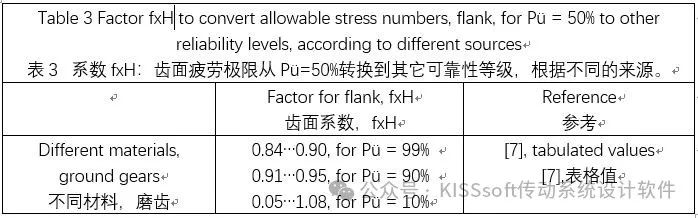
测量的齿面疲劳极限σHlim的标准差σ据报告(见参考文献9)是σ=2,8%(对深的渗碳层深,CHD)和σ=4.3%(对低CHD)。对于齿根疲劳极限σFlim的标准差σ报告,喷丸齿轮是σ=3.4%,未喷丸齿轮是σ=6.0%。(注意:标准偏差和应力使用了相同的符号σ)。这与齿轮喷丸报告中的值是一致的(见参考文献12),齿根疲劳极限σFlim的标准差是σ=3%。注意,这些值适用于S-N曲线的“无限寿命”部分。
计算示例:让我们考虑一个例子。假定σFlim=500MPa(如,具有高心部强度的渗碳淬火齿轮,质量等级MQ,见ISO6336-5的图10,线“MQ, a”)。这就意味着仅仅有1%齿轮的强度将会小于500MPa,并且有99%齿轮的强度会大于500MPa。让我们使用上面提到的标准差σ=6%(对于不喷丸齿轮,这是ISO6336-5图10的根本假定)。
假定正态分布,我们知道对于Pa=1%(Pu=99%)的负z-分数是z=-2.326(使用“负z分数表”,如,从参考文献13中可以找到这个值)。这就意味着在Pü=50%的σFlim平均值(试验中最初测量值)和Pü=99%的σFlim值之间存在-2.326σ的距离。(见图1中,Pa=50%和Pa=1%的灰色S-N曲线间的黑色垂直箭头,或:
σFlim(Pü=99%)=σFlim(Pu=50%)-2.326×6%×σFlim(Pu=50%),得到σFlim(Pu=99%)=0.86×σFlim(Pu=50%)。
从这里我们发现值
σFlim(Pu=50%)=σFlim(Pu=99%)/0.86=500MPa/0.86=581MPa。见垂直橙色,虚线(图2)表明齿根许用应力平均值581MPa。标准差σ是6%,因此(假定齿轮未喷丸)σ=35MPa(图3中水平蓝色箭头)。
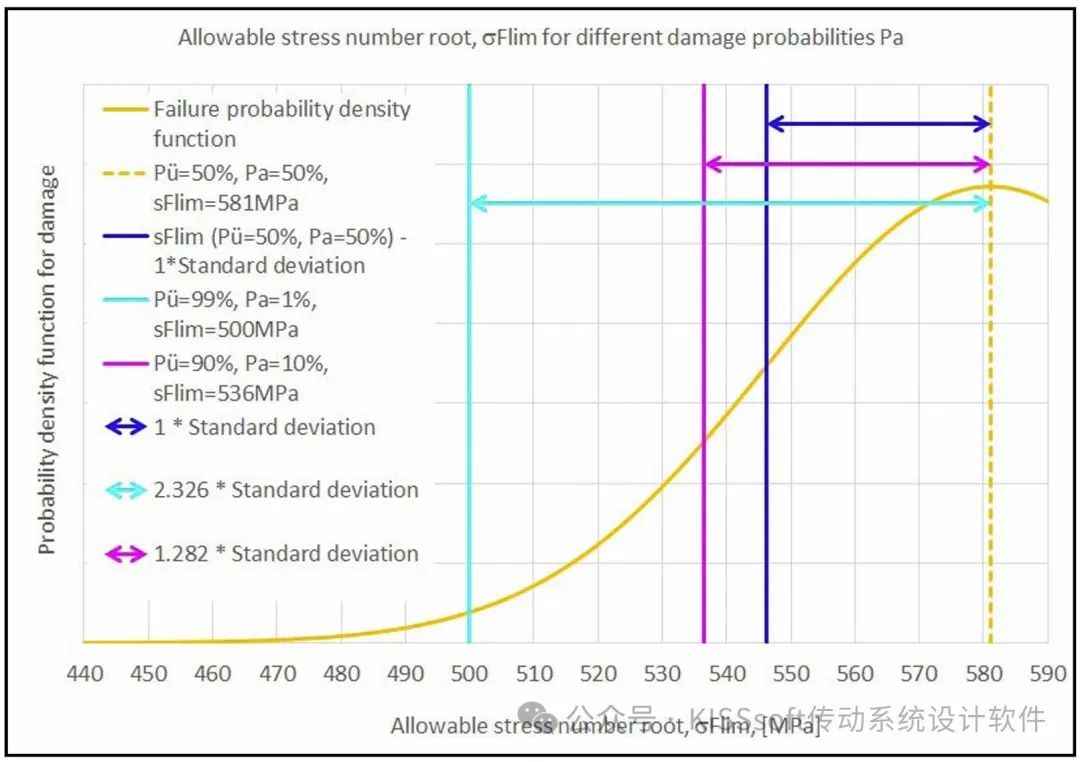
图3 疲劳极限的正态分布,不同可靠性的疲劳极限结果,标准差分布
疲劳极限的平均值(Pü=50%)σFlim= 581 MPa和Pa=1%(ISO 6336所用)的值之间的距离是
2.326×σ=2.326×35MPa=81MPa,图中用蓝绿色表示(见图3)。
于是,上面的系数fxF=0.86是没有的,但是,
fxF=1+z(Pa=1%)×σ=1-2.326×0.06=0.86(注意:z<0)。
如果我们现在想确定σFlim(Pü=90%),有时使用,例如,在车辆传动设计中,我们发现Pa=10%的z-分数(见参考文献13)是z=-1.282。从这个值我们能发现
σFlim(Pü=90%)=σFlim(Pü=50%)-1.282×6%×σFlim(Pü=50%)=581MPa(1-1.282×0.06)=536MPa。
见图3中表示了这个值,并且水平粉红色箭头长是:
∣z∣×σ=1.282×35MPa=44.7MPa。
比较和推荐:我们已经计算了渗碳淬火齿轮、未喷丸、Pa=10%的齿根许用应力σFlim(Pü=90%)=536MPa。这里通过依据ISO6336的基本值σFlim(Pü=99%)=500MPa来完成的,并且转换系数建立在测量强度值的标准差基础上。
现在我们将这个值与AGMA方法确定的值进行比较。这里,从Pa=1%到Pa=10%的转换系数KR=0.85(见表1)。如果我们在疲劳极限(依据ISO标准)中使用这个系数,那么σFlim(Pü=90%)将是:
σFlim(Pü=90%)=σFlim(Pü=99%)/KR=500MPa/0.85=588MPa。这个值比前面提到的数值536 MPa要高,因此,最好的情况是不那么保守,最坏的情况是不安全。虽然不能确定引用的文献或AGMA2101那个更值得信任,但有迹象表明,至少应谨慎使用KR值。
ISO 6336也提醒了用户这些可靠性系数。在允许使用的同时,它还指出“需要非常仔细的考虑这些调整,并且可能要求额外的、特定测试或用于推导可信的失效率的详细信息文件的出处。”这就意味着对一般工程师来讲,不鼓励通过简单的调整来得到不同的可靠性。
KISSsoft
KISSsoft是全球领先的齿轮传动系统设计和分析软件,具备所有类型齿轮箱及其零部件的设计能力,应用领域广泛,功能性强,技术全面。软件高度集成国际通用的各种机械标准,界面友好,以参数化的形式生成多种图形输出,被视为行业内的智能机械手册。